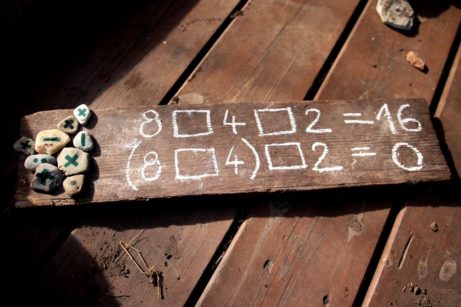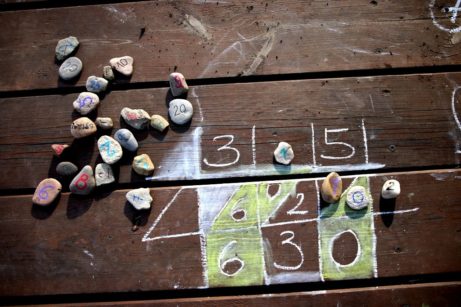HEJNÉHO METODA VENKU (3. třída)
PRINCIPY HEJNÉHO METODY
Rozvíjí náš mozek a navíc venku podpoří i naše tělo
Co je to Hejného metoda?
Lekce vznikla díky podpoře Nadace Vodafone Česká republika.
Za metodickou pomoc děkujeme Pavle Weizettel.
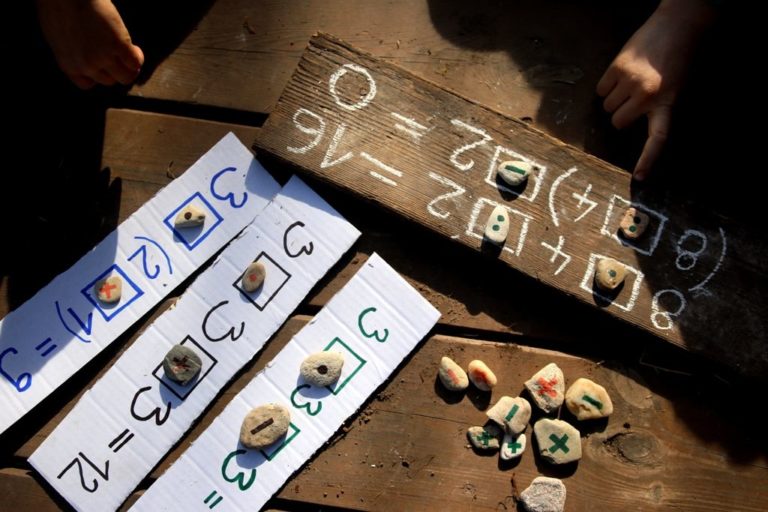
DOPLŇ ZNAMÉNKA
Stačí namalovat pár příkladů na chodník, kartón nebo prkno, ale vynechat znaménka (+ , - , x , / ). Na kameny namalujeme znaménka. Doporučujeme využít obě strany plochých oblázků. Děti mají za úkol umístit do příkladů znaménka, tak aby byl příklad správně.
Je přínosné zadat i dvojici podobných příkladů, které se liší jen použitím závorky. U dětí to přirozeně otvírá otázky a testování jaký mají závorky vliv na výsledek. Na závěr aktivity mohou děti vymýšlet vlastní příklady pro ostatní.
VĚTŠÍ, MENŠÍ, ROVNÁ SE
Kameny nabízí skvělou interaktivní hru. Stačí na papír/chodník napsat čísla/příklady, které chcete porovnávat. Na kameny si pak děti na jednu stranu namalují znaménko < na druhou stranu = . Pak už stačí jen umístit ty správné kameny/ znaménka k příkladům.
Pracovní list lze rychle zkontrolovat a kameny odstranit, aby mohlo pracovat další dítě/ skupina. Děti manipulace s kameny baví a v závěru mohou opět vymyslet vlastní příklady a napsat je pro ostatní na papír nebo na chodník.

TVARY V PRAXI
Zkuste s dětmi odhalit, kde je víc pravidelných pravoúhlých tvarů – ve městě či v přírodě? Jaké tvary najdeme spíše ve městě a které budou častěji v přírodě? Děti hledání tvarů venku baví. Najednou může být kvádr nebo krychle ohromných rozměrů.
Je skvělé využít městské budovy, značky, zastávky atd. Můžete připravit jednoduchý pracovní list a vyrazit hledat. Děti mohou předměty zakreslovat nebo ty menší přímo sbírat na pracovní list. V závěru hry porovnáme, na co která skupina přišla. Pokud máte čas a chuť, doporučujeme zkusit hledat venku i FRAKTÁLY (např. v listech kapradin).

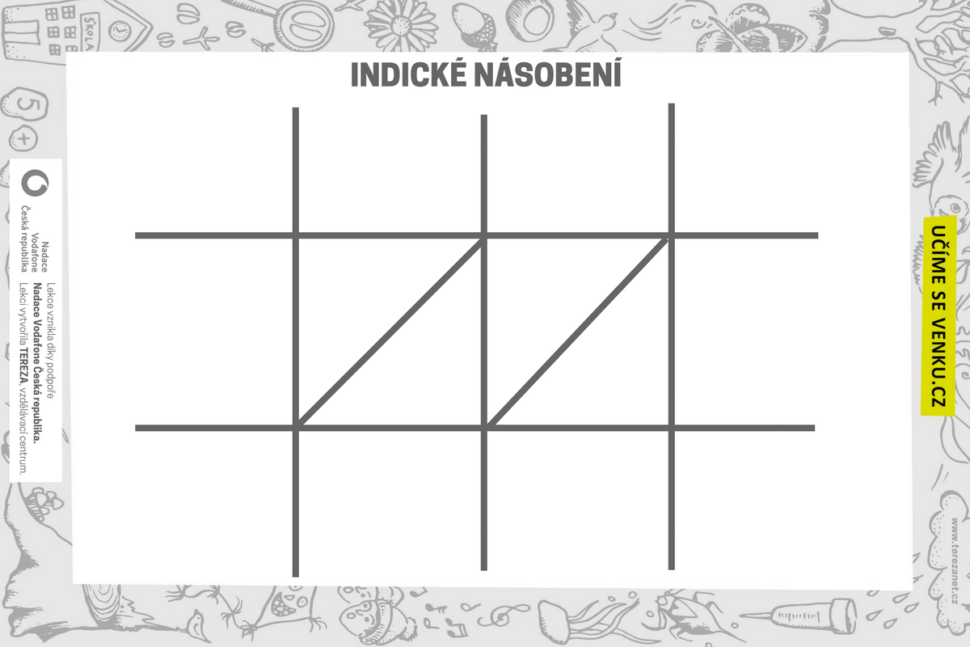
INDICKÉ NÁSOBENÍ
Je to jako kouzlo a děti jako kouzelníci. Pokud pochopí princip Indického násobení, zvládnou i velmi náročné příklady jen díky jednoduchému zápisu. Venku můžeme k zápisu využít opět kameny či křídu a chodník. Někteří kolemjdoucí budou jistě kroutit hlavou, co to ty děti počítají :).

KRYCHLE 1 LITR
Jak velký je jeden litr v krychli? Pro některé děti jsou představy v prostoru a převody jednotek snadné, pro jiné je to velmi náročné. Krychle o straně 10 cm, může pomoci. Stačí venku nastříhat větvičky dřevin (šetrně). Doporučujeme větvičky, které mají uvnitř přirozenou dutinku vyplněnou pěnovou dření (např. bez). Nejprve mohou děti samostatně nebo ve skupinách vymyslet kolik budou potřebovat větviček na čtverec, kolik na krychli. Pak si připraví větvičky dlouhé 10 cm - pokud budou spojovat drátky. (Pokud budou spojovat provázkem, je třeba mít větvičky delší). Kolik bude třeba drátků/ provázků? Drátky je vhodné mít delší, aby nevypadávaly. Najednou je pro děti představa 1 litru v krychli jasnější.

KRYCHLE 1 KUBÍK
Jak velký je jeden litr v krychli? Pro některé děti jsou představy v prostoru a převody jednotek snadné, pro jiné je to velmi náročné. Krychle o straně 10 cm, může pomoci. Stačí venku nastříhat větvičky dřevin (šetrně). Doporučujeme větvičky, které mají uvnitř přirozenou dutinku vyplněnou pěnovou dření (např. bez). Nejprve mohou děti samostatně nebo ve skupinách vymyslet kolik budou potřebovat větviček na čtverec, kolik na krychli. Pak si připraví větvičky dlouhé 10 cm – pokud budou spojovat drátky. (Pokud budou spojovat provázkem, je třeba mít větvičky delší.) Kolik bude třeba drátků/provázků? Drátky je vhodné mít delší, aby nevypadávaly. Najednou je pro děti představa 1 litru v krychli jasnější.

1 METR = 10 DECIMETRŮ
Co je kolem nás velké 1 m? Kolik se vejde decimetrů do metru? Jak dlouhých je 10 metrů? Všechny tyto míry můžeme venku zažít v praxi. Stačí si připravit pro každé dítě/do skupiny proutek 1 m dlouhý.
- Děti změří sebe, kde na svém těle mají výšku 1 m?
- Děti samostatně/ve skupině chodí a měří co je vetší, či menší než 1 m.
- Děti společně zkouší, jak dlouhá je 10 m dlouhá cesta (10 proutků za sebou).
- Z proutků můžeme tvořit různé cesty, obrazce a labyrinty.
- Nastříháme tenké větvičky po 10 cm a znovu seskládáme 1 m z 10 decimetrů.
- Můžete si vymýšlet další své hry s mírami v prostoru.

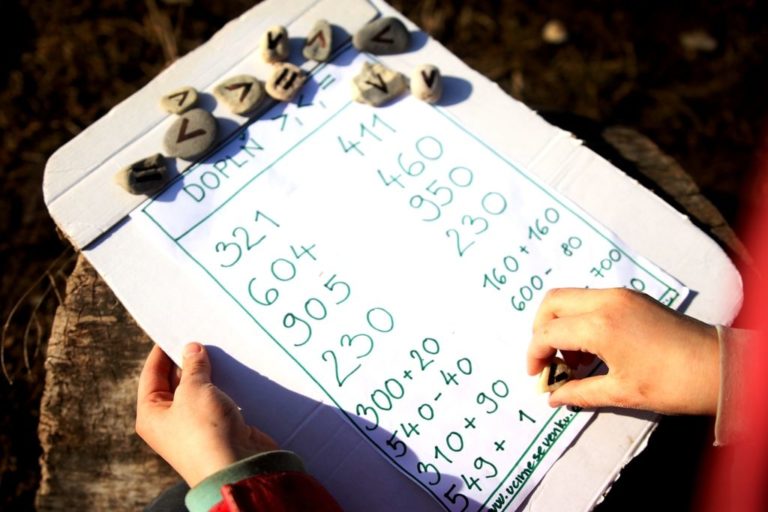
VÝSTAVIŠTĚ VENKU
Výstaviště je skvělá aktivita v Hejného metodě, děti moc baví a tak jsme si ji zkusili vymyslet i ven. Úkolem je v zadaném plánu, kde jsou jen některá čísla, najít řadu čísel tak, aby na sebe navazovaly. Nejprve jsme zkoušeli větvičky zapíchnuté v zemi s kamínky + provázek, který se přiváže k číslu 1. Pak jsme testovali čísla na kartónech a dokonce vyráběli i výstaviště na platu od vajíček nebo prkénku. Děti ohromně bavilo vymýšlení, vyrábění (především o zatloukání hřebíků byl boj) i testování. Nejprve mohou děti pracovat se zadáním z učebnice či pracovního sešitu. Ale ještě lepší je, když si vymýšlí úkoly navzájem.
Tip: Nakonec se nejvíce osvědčilo výstaviště na dřevěné stěně zahradního domku. Je stále po ruce a nikdo na něj nemůže omylem šlápnout.

NÁSOBILKA NA OČÍCH
Pomocná tabulka násobení je pro děti skvělý pomocník. Když byl při vyrábění destičky pro výstaviště (viz výše) tak velký zájem o zatloukání, rozhodli jsme se s dětmi vyrobit velkou hrací tabulku násobení. Zatlouci přesně 100 hřebíčků byla výzva. Domlouvání, vyměřování a střídání v zatloukání rozvíjelo mnoho dovedností u dětí i dospělých. Pak se připravovali kartičky z kartónu, psala se čísla a pak už se mohlo hrát. Děti si navzájem vymýšlely různé úkoly. Zájem po pár dnech opadl, ale tabulka je stále na očích a při počítání se k ní děti vrací a někdy si znovu navzájem připravují úkoly.

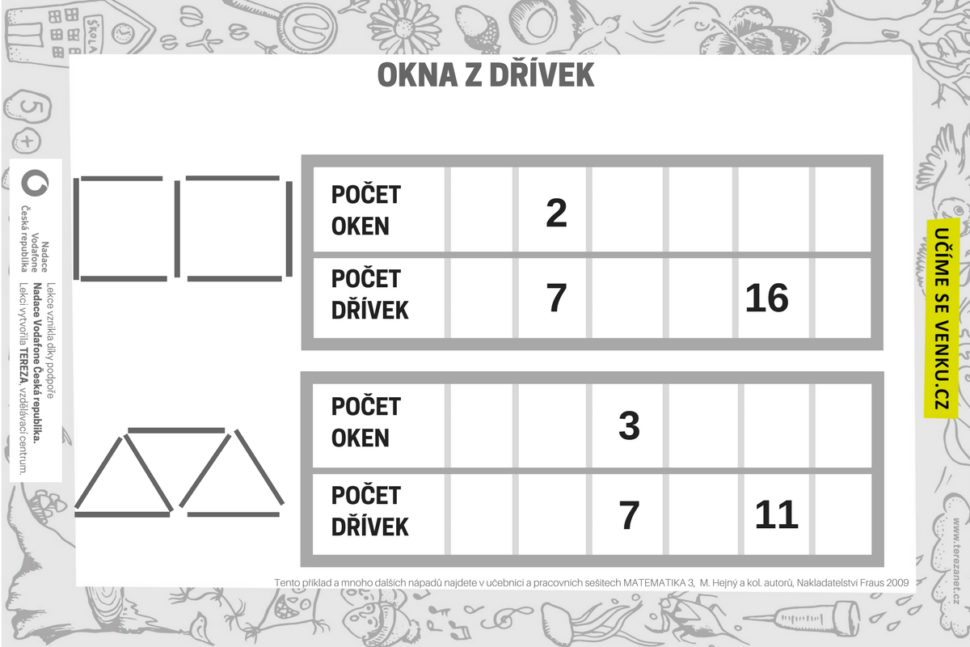
OKNA Z VĚTVIČEK
Jak roste počet dřívek s narůstajícím počtem oken? Hravá úloha z učebnice pro 3. třídu nás moc bavila. Děti použili dřívka z předchozích her a tak někoho ve skupině bavilo skládání oken, jiného počítání dřívek, někoho zapisování do pracovního listu. Jednoduchá hra na ven nebo si lze venku připravit větvičky do třídy.

PAVUČINY
Prostředí pavučin rozšiřuje prostředí hadů o geometricky bohatší zápis (doplněný někdy i barvou). Pro děti i dospělé je to na začátku oříšek, ale jakmile odhalí princip, stávají se z nich agenti, kteří luští tajné šifry.
Zkoušeli jsme pavučiny na papíru s doplňováním kamenů, pavučiny nakreslené i dopisované křídou, ale nejvíc děti bavily barevné pavučiny, kde doplňovaly čísla na kamenech. Kameny se snadno přesouvaly a tak se děti snadno střídali.

STAVÍME MOSTY A VĚŽE
Cíl je jednoduchý – otestovat své konstruktérské dovednosti při stavbě. Toto může být opravdová výzva. Postavit most přes vodu, díru nebo přes propast, kterou vidíme ve fantazii. Příroda nabízí mnoho příležitostí i stavebního materiálu. Nechte stavbu vést děti, ať si vyzkouší své plány, nápady i zažijí neúspěchy. Najít vlastní chyby je skvělá příležitost, jak se zdokonalit. Zdánlivě odpočinková aktivita rozvíjí mnoho prostorových dovedností.

OHLÉDNUTÍ
CÍL: Společně se ohlédnout za vším, co jsme zažili a objevili. Zhodnotit, co se nám líbilo a co příště zopakujeme. Doporučujeme tuto část nevynechat. Ať jste venku vyzkoušeli jakékoliv hry a prostředí, zhodnoťte s dětmi svou práci i zážitky. Můžeme využít hlavičky postaviček a vést rozhovor nebo zhodnotit i bez jejich pomoci. Nápady můžete společně zapsat, či zakreslit. Je skvělé pokud se vám podaří zkoušet matematiku venku pravidelně. Vyplatí se, když každý za sebe doplní následující nedokončené věty:
- Nejsilnější zážitek pro mě byl...
- Naopak se mi nelíbilo a chtěl by příště změnit...
- Během her mě napadlo...
Za metodickou pomoc s Hejného metodou děkujeme PAVLE WEINZETTEL
Nové matematické hry ven jsme otestovali i díky podpoře NADACE VODAFONE
v rámci programu Rok jinak. Děkujeme!

BAVÍ VÁS MATEMÁG?
POZVĚTE HO VEN.
Matemág je víc než jen digitální hra. Je to magický nástroj, který dává radost z objevování světa čísel a navíc při matematickém bádání propojuje děti s rodiči. Teď ho můžete hrát i naživo.
VYZKOUŠEJTE I DALŠÍ LEKCE

HEJNÉHO METODA VENKU (1.tř)
Zažít matematiku jinak. Vyzkoušet Hejného metody i venku. Co je to Hejného metoda?
ČAS: 10 - 60 min., VĚK: 1.st. ZŠ, MÍSTO: vhodná lokalita kolem školy. OBDOBÍ: celoročně

AUTOBUS
CÍL: Prožít sčítání a odčítání na vlastní kůži, nebo alespoň na vlastní ruce a oči. Za pomoc s lekcí děkujeme Pavle Weinzettel.
ČAS: 20 - 40 min., VĚK: 1.st. ZŠ, MÍSTO: lokalita kolem školy OBDOBÍ: celoročně

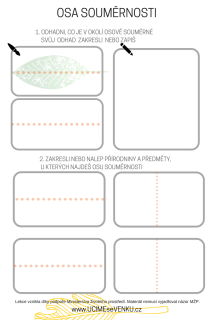
OSA SOUMĚRNOSTI
CÍL: Vyzkoušet si hledat osu souměrnosti v přírodě i ve městě. ČAS: 20 min., VĚK: 1.st. ZŠ, MÍSTO: lokalita kolem školy s možností hledat přírodniny nebo pozorovat budovy, OBDOBÍ: celoročně
Nejnovější články