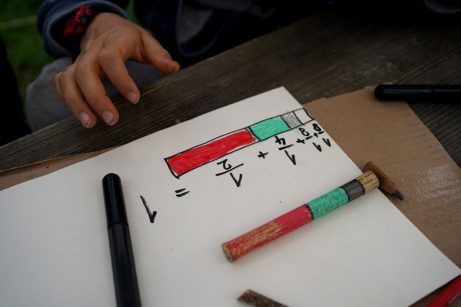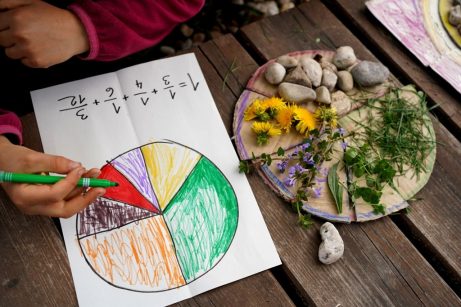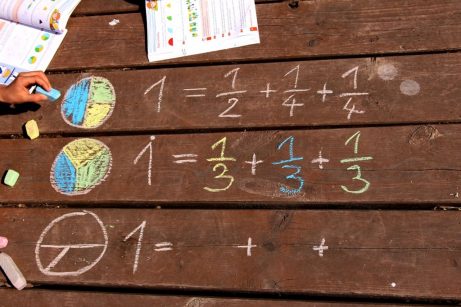ČÍSLA VENKU
Měříme
1 AR
LITR a KUBÍK venku
Zlomky
venku
Zlomky ve sklenici
Zlomková pizzerie
Skákavé
zlomky
Hejného metoda venku
pro 3. třídu
Zažít matematiku jinak. Vyzkoušet Hejného metody venku nejen s 3. třídou. Co je to Hejného metoda?

Výlet
s Matemágem
Matemág je víc než jen digitální hra. Je to magický nástroj, který dává radost z objevování světa čísel a navíc při matematickém bádání propojuje děti s rodiči. Teď ho můžete hrát i naživo.

Letokruhy

Venkovní počítadla

Sčítání, odčítání, řady a symboly čísel, lze snadno a hravě trénovat i venku. Děti pracují s různorodým materiálem, mohou se víc pohybovat, práce je pak více baví, je lépe představitelná. Počítejte např. 1. Větvičky, listy, dlaždice, stromy kolem školy. 2. Kameny, na které dopíšete symboly čísel, sčítání, odčítání a rovná se. 3. Kartičky z kartónu, které jsou poschovávané mezi stromy, a děti mají za úkol poskládat řadu čísel.
Pomůcky: přírodniny, tužka, křída, fix
Věk: MŠ, 1.– 3. ročník ZŠ
Čas: 5 - 30 minut, kdy: celoročně
Výroba geodestičky

Odřezky dřevěných prken je nejprve třeba oříznout do vhodného tvaru a zapilovat. Následuje zakreslení čtvercové sítě pro hřebíčky. Na závěr oblíbené zatlučení hřebíčků (nejlépe s co nejmenší hlavičkou, např. kolářské). Pak už stačí nasazovat gumičky, dle fantazie či zadání.
Pomůcky: odřezky prken, kladívko do skupiny, hřebíčky, gumičky
Věk: MŠ, 1. - 2. třída ZŠ
Čas: 20 - 40 minut, kdy: suché dny
Čísla
v letokruzích

Pařezy s letokruhy nabízí dobré příležitosti k počítání. Nejsnadnější úkol je spočítat, kolika let se strom dožil (pro kontrolu lze barevně označit výročí 10, 20, 30 let...). Ale to je jen začátek. Pak mohou skupinky dětí vypočítat, v kterém roce strom začal růst (pokud víme, kdy byl strom pokácen). Koho bude lákat, může označit letokruhy, kdy se odehrály významné události (narození žáků, revoluce, války atd.).
Pomůcky: pařez se zřetelnými letokruhy, (pastelky)
Věk: 2. - 5. třída ZŠ
Čas: čas: 10 - 30 minut, kdy: kdykoli
Provázkový pravý úhel

Jako problémovou úlohu nechte žáky vytvořit jen pomocí provazu pravý úhel. Jejich úkolem je na provaze pomocí uzlíků vyznačit tolik stejných dílků, kolik jich budou potřebovat k tomu, aby z provazu vytvořili pravoúhlý trojúhelník.
Pomůcky: provaz dlouhý 5m (švihadlo)
Věk: 7. – 9. ročník ZŠ, SŠ
Čas: 30 minut, kdy: celoročně
Procenta
v zahradě

Na stůl nebo deku v zahradě umístíme 10 (20) různých přírodnin ze zahrady (například 4 šišky, 2 listy, 5 kamenů, 2 květiny, 3 ulity a 4 kaštany apod.). Žáci nechť počítají procenta zastoupení jednotlivých skupin přírodnin (např. kolik procent šišek je mezi přírodninami?). Nebo naopak, řekneme procento a žáci přijdou na to, která skupina mu odpovídá (např. čeho je 25 %?).
Věk: 5. - 8. třída ZŠ
Čas: 45 minut kdy: celoročně
Zlomky
v zahradě

Zadejte žákům, aby sklenice, které jsou všechny stejné, naplnili pískem (vodou, hlínou); první do ¼, další do ⅓, další zase do ½ apod. K tomu, aby zjistili, kde je polovina (třetina, čtvrtina), ať využijí zbývající sklenice (rozdělí obsah na poloviny, na třetiny). Pak je nechte zlomky ve sklenicích sčítat a odečítat (sklenice odsypávat a sesypávat).
Pomůcky: 10 - 30 stejných sklenic (zavařovací), pískoviště, rybníček nebo nevyužívaný záhon
Věk: 6. - 8. třída ZŠ
Čas: 40 minut, kdy: celoročně
Souměrnost letokruhů

Obvod a průměr kruhu

Inspirujte nás i ostatní, jak tvoříte venku VY?